BDD Visualizer Tutorial - Part 2

This is part 2 of a tutorial designed to help you use the BDD Visualizer, a tool that can generate visualizations of Reduced Ordered Binary Decision Diagrams (BDDs).
The BDD Visualizer is located here: http://www.cs.uc.edu/~weaversa/BDD_Visualizer.html.
In part 2 of the tutorial we will use BDDs to solve a very simple Bounded Model Checking problem.
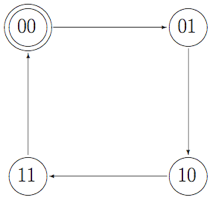
Here we have a state machine of a two-bit counter.
We would like to know:
Does this two-bit counter always reach state 11 in exactly three time steps?
The first thing we need to do is to create variables which will represent the individual bits of the counter at each time step. We will name these variables v_b_t, where b ∈ {0, 1} and t ∈ {0, 1, 2, 3}.
We can express the starting state of the two-bit counter with the following constraint:
and(not(v_1_0), not(v_0_0)) ;Initial state is 00
This constraint forces our counter to take value 00 at time step 0.
We will now describe all possible state transitions:
equ(v_1_1, xor(v_0_0, v_1_0)) ;00 -> 01
equ(v_0_1, not(v_0_0))
equ(v_1_2, xor(v_0_1, v_1_1)) ;01 -> 10
equ(v_0_2, not(v_0_1))
equ(v_1_3, xor(v_0_2, v_1_2)) ;10 -> 11
equ(v_0_3, not(v_0_2))
Our two-bit counter is now fully specified.
The last step is to describe the property that we want to hold, namely, that the two-bit counter must reach state 11 in exactly three time steps:
and(not(and(v_1_0, v_0_0)), ;Time step 0 is not 11
not(and(v_1_1, v_0_1)), ;Time step 1 is not 11
not(and(v_1_2, v_0_2)), ;Time step 2 is not 11
and(v_1_3, v_0_3) ;Time step 3 is 11
)
Conjoining the entire formula together, we get:
print(
and(
;Specification of the two-bit counter
and(not(v_1_0), not(v_0_0)) ;Initial state is 00
equ(v_1_1, xor(v_0_0, v_1_0)) ;00 -> 01
equ(v_0_1, not(v_0_0))
equ(v_1_2, xor(v_0_1, v_1_1)) ;01 -> 10
equ(v_0_2, not(v_0_1))
equ(v_1_3, xor(v_0_2, v_1_2)) ;10 -> 11
equ(v_0_3, not(v_0_2))
;Negate the property we want to prove
not(and(not(and(v_1_0, v_0_0)), ;Time step 0 is not 11
not(and(v_1_1, v_0_1)), ;Time step 1 is not 11
not(and(v_1_2, v_0_2)), ;Time step 2 is not 11
and(v_1_3, v_0_3) ;Time step 3 is 11
))))
Notice that the property we want to prove has been negated. This is a common practice which will cause the BDD to be exactly F if and only if the property we want to prove is true.
The result of submitting this example is the following visualization:
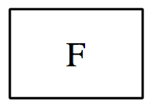
This result means that the property we tested does hold, i.e. the two-bit counter will always reach state 11 in exactly three time steps.
But, what will happen if we have a bug in our set of constraints?
Well, let’s try it out:
order(v_0_3, v_1_3, v_0_2, v_1_2, v_0_1, v_1_1, v_0_0, v_1_0)
print(
and(
;Specification of the two-bit counter
and(not(v_1_0), not(v_0_0)) ;Initial state is 00
equ(v_1_1, xor(v_0_0, v_1_0)) ;00 -> 01
equ(v_0_1, v_0_0) ;BUG - Whoops! Forgot the not()
equ(v_1_2, xor(v_0_1, v_1_1)) ;01 -> 00
equ(v_0_2, not(v_0_1))
equ(v_1_3, xor(v_0_2, v_1_2)) ;10 -> 11
equ(v_0_3, not(v_0_2))
;Negate the property we want to prove
not(and(not(and(v_1_0, v_0_0)), ;Time step 0 is not 11
not(and(v_1_1, v_0_1)), ;Time step 1 is not 11
not(and(v_1_2, v_0_2)), ;Time step 2 is not 11
and(v_1_3, v_0_3) ;Time step 3 is 11
))))
The result of submitting this example is the following visualization:
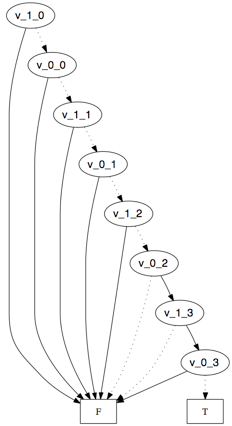
This clearly shows that there is only path from the root node to the T leaf.
This means that there is only solution that satisfies our set of constraints, namely:
v_1_0 = 0, v_0_0 = 0 -- 00
v_1_1 = 0, v_0_1 = 1 -- 00
v_1_2 = 1, v_0_2 = 0 -- 01
v_1_3 = 1, v_0_3 = 1 -- 10
From this solution we can clearly see that our counter does not transition correctly. Specifically, we see that the transition from time step 0 to 1 is incorrect. This points us directly to the bug we inserted in the specification above.